Fibonacci2
Die Fibonacci-Folge wird in der Regel als Spirale innerhalb eines Rechtecks, welches aus Quadraten zusammengesetzt wird, dargestellt. Anders ausgedrückt: Diese Spirale mit den dargestellten Eigenschaften wird durch die Fibonacci-Folge beschrieben.
Das sieht zum Beispiel so aus:
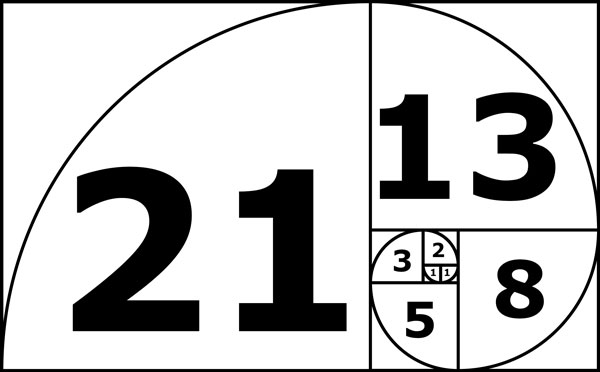
Bei dieser genialen Darstellungsweise werden die Fibonacci-Zahlen als Seitenlänge für Quadrate verwendet. Diese werden dann im oder gegen den Uhrzeigersinn angeordnet und durch Viertelkreise mit dem Radius der jeweiligen Fibonacci-Zahl verbunden. So entsteht die Fibonacci-Spirale. Hier habe ich noch die Schriftgröße der Fibonacci Zahlen im Fibonacci-Verhältnis ansteigen lassen.
Die Idee für eine neue Fibonacci-Illustration war, die Fibonacci-Folge selbst als Quadrat darzustellen. Der Nautilus entsteht dadurch, dass die Fibonacci-Zahlen in der geometrischen Darstellung quadriert werden. Es werden dabei also nicht die eigentlichen Fibonacci-Zahlen in den Einzelflächen dargestellt, sondern deren Quadratur. Verzichtet man auf die geometrische Quadratur der Fibonacci-Zahlen und reiht entsprechend viele gleich große Quadrate aneinander, entsteht das hier dargestellte „Fibonacci-Quadrat“.
Wenn Sie noch nicht genau wissen, was der Goldene Schnitt oder die Fibonacci-Folge ist, können Sie zuerst weiter unten nachlesen:

Das Fibonacci-Quadrat
In der Grafik ist die Fibonacci-Folge durch die Anzahl der einzelnen Quadrate dargestellt. Der Goldene Schnitt ist durch die Grauwerte dargestellt. In der Mitte fängt es mit weiß (Grauwert null) an. Es folgen ab f1 immer Quadrate mit den Grauwerten 38,19660113 (Minor), 61,80339887 (Mayor) und 100 (Summa). Auch die Trennlinien, die die einzelnen Quadrate und die Fibonacci-Zahlen von den benachbarten Fibonacci-Zahlen optisch abgrenzen sind immer nach der Minor-Mayor-Systematik mit den entsprechenden Grauwerten gestaltet.
Quadrat ohne äußere Quadratzahl?!
Als ich die Idee hatte, aus der Fibonacci-Folge ein Quadrat zu erstellen, war schnell klar, dass f1 = 1 und f12 = 144 die einzigen Quadratzahlen sind. Diese wenigen Iterationen waren mir optisch nicht ansprechend genug. Daher musste nach Erreichen des perfekten 12 x 12 Quadrates mit f10 (Summe gleich 144 (f12), die geometrische Exaktheit zugunsten der grafischen Darstellung etwas zurückstehen.
Bekanntlich sind die Summen der Fibonaccizahlen immer um 1 kleiner als die jeweils übernächste Fibonaccizahl (∑fn = fn+2-1). Dadurch kann nur bei der grafischen Darstellung der Null (mit dem gleichen Rauminhalt wie jedes einwertige Quadrat) zu Beginn der Folge in f10 auch die Quadratzahl 144 als Quadrat dargestellt werden.
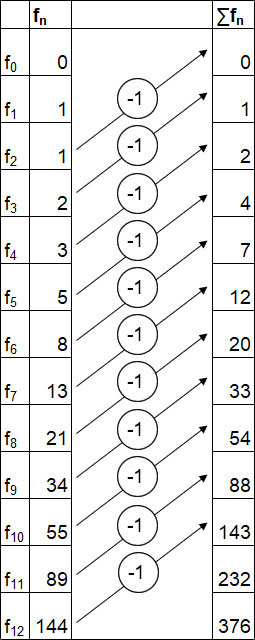
Deutlich wird dies auch durch folgende Darstellung. Auch wenn die Null aufgeführt wird, gibt es keine Stelle, in der die Summe der Fibonaccizahlen nicht um 1 kleiner ist als die übernächste Fibonaccizahl. Nur weil die Null in der Grafik eine Fläche bekommen hat, lässt sich das Quadrat (12 x 12) darstellen.
Da die Fibonacci-Folge außer in f1 und f12 keine Quadratzahlen enthält, ist das Quadrat, wenn man nach f10 (∑=144) weiterzeichnet nie vollständig beendet.
Die Seitenlängen sind oft gleich lang, aber die letzte Seite schließt sich zwangsläufig nicht mehr. Unter diesen Voraussetzungen hat das vorliegende Fibonacci-Quadrat in folgenden Iterationen die gleiche Höhe und Breite:
f17, f16, f15, f13, f10, f7, f5, f6, f4, f0
Für diese Darstellung kommt es mir nicht darauf an, dass die Breite und Höhe des Quadrates immer gleich sind. Diese Illustration stellt das Fibonacci-Quadrat bis f18 dar. f18 ist willkürlich gewählt. Mir gefiel die Optik aber für einen Druck in einer Größe mit einem Quadratzentimeter je Quadrat am besten.

Der Fibonacci-Nautilus
Der Nautilus entspricht an der außen verlaufenden Kante der üblichen Darstellung der Viertelkreise der quadrierten Fibonacci-Zahlen. Im Breitenverlauf und Verlauf der Grauwerte ist wieder das Konzept des Goldenen Schnitts umgesetzt. So ist beispielsweise bei 38,1966% der Strecke auch 38,1966% des Grauwertes und der Breite der Form erreicht. Oder anders ausgedrückt: Die Formbreite und die Grauwerte entsprechen jeweils der Summe der Werte beider vorhergehenden Fibonacci-Zahlen. Wobei 100% (schwarz) bei f1 liegt

Die Kombination von Fibonacci-Quadrat und Fibonacci-Nautilus im Goldenen Schnitt
In der finalen Umsetzung wird das „Quadrat“ noch mit dem Konzept des Goldenen Schnitts kombiniert.
Die vollständige Illustration Fibonacci2 mit „Fibonacci-Quadrat“ und „Fibonacci-Nautilus“ verbindet das Konzept des Goldenen Schnitts mit der Fibonacci-Folge grafisch.
Zwei Fakten: Der Fibonacci-Nautilus entsteht durch die Ergänzung immer weiterer Quadrate der Fibonacci-Zahlen.
Die Quotienten zweier benachbarter Fibonaccizahlen nähern sich mit jeder Iteration der Fibonacci-Folge alternierend dem Goldenen Schnitt bzw. der Goldenen Zahl. Allerdings handelt es sich dabei nicht um eine unendliche Annäherung ohne den Schnittpunkt zu treffen. Vielmehr oszilliert der Wert um den Goldenen Schnitt.
Deshalb nähert sich die Gesamt-Illustration bei jeder Iteration, in der Höhe und Breite des Fibonacci-Quadrates gleich sind dem Goldenen Schnitt. Dies ist auch evident, da die Erweiterung einer Fibonacci-Spirale um eine Iteration nur ein weiteres Quadrat mit der Seitenlänge der jeweils nächsten Fibonacci-Zahl erfordert. Daher ist auch klar, dass durch die Kombination des Fibonacci-Quadrates, welches auf die Quadrierung der Fibonacci-Zahlen zur grafischen Darstellung verzichtet, mit dem Fibonacci-Nautilus, eine Gesamt-Illustration entsteht, die dem Goldenen Schnitt (nahezu) entspricht.
So repräsentiert diese Darstellung der Fibonacci-Folge in Kombination mit dem Goldenen Schnitt in mehrfacher Weise die, in der Natur vorkommenden mathematisch-physikalischen Gesetzmäßigkeiten in grafischer Form.
Die Fibonacci-Folge
Die so genannten Fibonacci-Zahlen sind nach Leonardo da Pisa benannt, der auch Fibonacci (von Filius Bonacci) genannt wurde. Die Namensgebung für die bekannte unendliche Folge von natürlichen Zahlen basiert allerdings nicht auf der Entdeckung dieser Folge durch Fibonacci. Tatsächlich war diese Folge schon ca. 1.000 Jahre vor Leonardo bekannt. Edmund Weitz, Professor für Mathematik skizziert dazu in seinem populären Buch „Gesichter der Mathematik“ eine interessante Sichtweise indem er argumentiert, dass die Zuschreibung der Folge auf Leonardo auch deshalb unglücklich sei, weil er eine deutlich größere Bedeutung in der Mathematik hatte, als diese „lustige Aufgabe über Kaninchen“. Er bezieht sich dabei auf das Hauptwerk Leonardos mit dem Titel „Liber abbaci“:
„Sowohl vom Umfang der abgedeckten Themen her als auch unter didaktischen Aspekten übertraf es bei weitem andere Texte aus der Zeit und auch die meisten aus den Jahrhunderten danach. Methoden und Rechentechniken wurden darin nicht nur vorgeführt, sondern erklärt und begründet. Insbesondere wurde von Leonardo auch die indisch-arabische Zahlenwelt (also: „unser“ Dezimalsystem) vorgestellt und popularisiert. Wahrscheinlich hatte Fibonacci in Europa einen noch größeren Einfluss auf die Entwicklung der Mathematik und damit der gesamten Kultur als al-Chwarizmi, mit dessen Schriften er übrigens vertraut war.“
Leonardo da Pisa beschrieb mit dieser Folge allerdings einen natürlichen Prozess: Die Populationsentwicklung (von Kaninchen). Wie sich später zeigte, stieß Fibonacci damit auf eine Beschreibung, die für viele Wachstumsprozesse in der Natur gültig ist.
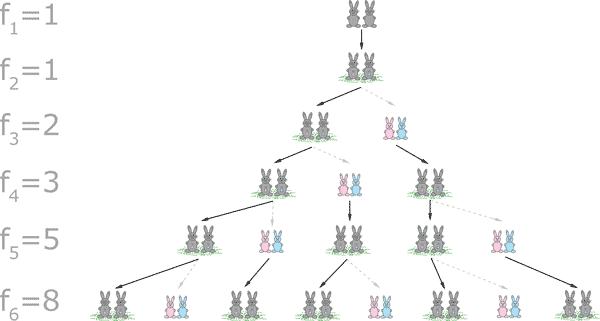
Die Fibonacci-Folge beginnt mit einem Kaninchen-Paar. Dieses Paar bekommt im übernächsten Monat ein neues Paar als Nachwuchs. Danach bekommt das Ursprungspaar jeden Monat ein neues Paar als Nachwuchs. Dieses Prinzip gilt ebenso für alle Nachwuchspaare. Immer bleiben die Paare im ersten Lebensmonat ohne Nachwuchs und danach werfen sie jeden Monat ein neues Paar. Außerdem hat Fibonacci für diese beispielhafte Erklärung der Folge die Bedingungen aufgestellt, dass das erste Paar einfach vorhanden ist und dass kein Paar flüchten oder von außen hinzukommen kann und dass kein Paar jemals stirbt. An der Entwicklung der Fibonacci-Zahlen in den Generationen sieht man daher auch, dass der Tod in der belebten Natur seine Notwendigkeit darstellt.
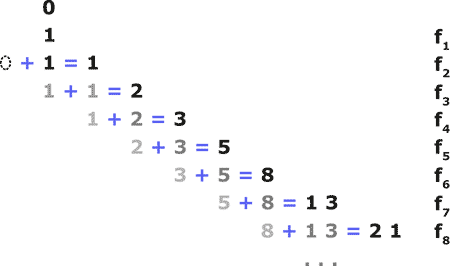
Mathematisch ausgedrückt beginnt die Folge also mit zwei Einsen. Gegenwärtig wird auch noch eine Null vor den ersten beiden Einsen notiert. Die Folge selbst ergibt sich dann aus der Addition des aktuellen Wertes mit dem vorhergegangenen Wert. Diese Summe ist der nächste Wert in der Fibonacci-Folge. Oder anders ausgedrückt: Jede Fibonacci-Zahl ist die Summe ihrer beiden Vorgänger:
Die Fibonacci-Zahlen werden üblicherweise mit der folgenden Schreibweise nummeriert. Die Nummerierung beginnt bei der ersten Eins. (Wer sich darüber wundert, hat aufmerksam gelesen. Es gibt auch die f0 und sogar negative Fibonacci-Zahlen wie f-1, f-2… Dies wird in diesem Rahmen aber nicht thematisiert).
- 1 = erste Fibonacci-Zahl = f1
- 1 = zweite Fibonacci-Zahl = f2
- 2 = dritte Fibonacci-Zahl = f3
- …
So ist immer klar, das f3 = den Wert 2 hat, f7 = den Wert 13 hat usw.
Fibonacci-Folgen in der Natur
Neben der mathematisch theoretischen Beschreibung für Wachstumsprozesse ist die Fibonacci-Folge auch an vielen Stellen der Natur direkt erkennbar.
Die Beschreibung dieser Phänomene lässt sich mit der berühmten Kaninchendarstellung erklären. Anstelle der variablen „Kaninchenpaar mit Nachwuchs“ und „Kaninchenpaar ohne Nachwuchs“ treten andere Variablen, die aber immer dem Mechanismus der Fibonacci-Zahlen folgen.
Pflanzen ordnen Blätter und Früchte häufig in Spiralen an, deren Anzahl Fibonacci-Zahlen darstellen. Diese Anordnung garantiert die beste Lichtausbeute und sorgt dafür, dass aufgrund der Eigenschaften der Fibonacci-Folge Blätter, die so angeordnet sind, sich nie gegenseitig das vollständige Licht wegnehmen können.
Die Anzahl der Vorfahren einer Drohne (männliche Honigbiene) entspricht aufgrund einer genetischen Besonderheit immer den Fibonacci-Zahlen.
Chemische Verbindungen folgen zum Teil genau den Fibonacci-Zahlen.
Die Folge taucht auch in der Musik und in der Astronomie auf.
Viele interessante Gesetzmäßigkeiten wurden in der Folge schon entdeckt und es kommen immer neue hinzu.
Das alles ist vielfach erzählt und beschrieben, wie z.B. bei Youtube, wenn man diese Videonummer dort in die Suche eingibt: R8w4l3f3g58
Der goldene Schnitt
Mit dem Goldenen Schnitt wird ein ganz bestimmtes Teilungsverhältnis beschrieben. Am einfachsten lässt sich der Goldene Schnitt zunächst an der Teilung einer Strecke erläutern.
Soll eine Strecke so in zwei Teile „geschnitten“ werden, dass das Ergebnis dem Goldenen Schnitt entspricht, dann lautet die Aufgabe:
Teile eine Strecke so in zwei Teile, dass das Größenverhältnis der kleinen Strecke zur großen Strecke identisch ist mit dem Größenverhältnis der großen Strecke zur Gesamtstrecke.
Durch die Teilung der Strecke in zwei Teile erhält man drei Werte:
- Kleine Teilstrecke (Minor)
- Große Teilstrecke (Major)
- Gesamtstrecke (Summa)
Grafisch sieht das z.B. so aus:
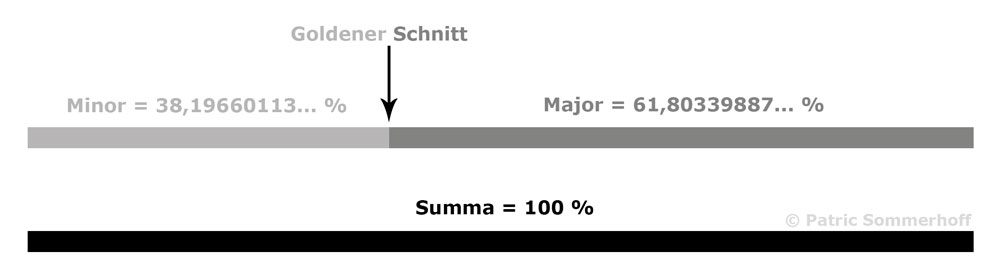
In einer formalen Schreibweise sieht es so aus:
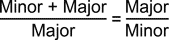
bzw.
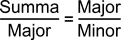
und
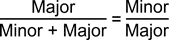
bzw.
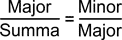
Die Goldene Zahl Phi
Die Goldene Zahl Phi Φ ist die formale Darstellung des Goldenen Schnittes. Die erste Beschreibung der Goldenen Zahl wird Euklid zugeschrieben.
Diese formale Darstellung ist identisch mit der oben vorgestellten Schreibweise für die Größen Minor, Major und Summa, verwendet aber die allgemeinere algebraische Schreibweise. Also zum Beispiel:
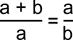
Die Strecke Major wäre in der obigen Grafik a, Minor wäre b.
Dass immer das gleiche Teilungsverhältnis entsteht, kann man sehr schön sehen, wenn man die goldenen Zahl Phi selbst in die Formel einsetzt:
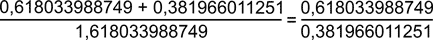
Noch anschaulicher so:
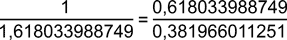
Wer sich für die mathematische Herleitung der Zahl Phi genauer interessiert, dem sei diese Seite empfohlen, auf der auch weitere Eigenschaften von Phi angesprochen werden oder etwas formaler in die Tiefe gehend bei Wikipedia. Eine anschauliche Darstellung des Goldenen Schnitts (auch wenn mir bei manchen Erklärungen relativierende Anmerkungen (z.B. in Bezug auf Mekka) fehlen) findet man z.B., indem man bei Youtube diese Videonummer dort in die Suche eingibt: MyVaGOEt6MQ
Fibonaccizahlen und der Goldene Schnitt
Wie bereits weiter oben angedeutet, gibt es einen direkten Zusammenhang zwischen den Zahlen der Fibonacci-Folge und dem Goldenen Schnitt, bzw. der Goldenen Zahl.
Dividiert man aufeinander folgende Werte der Fibonacci-Folge, nähert sich der Quotient der Goldenen Zahl. Hier der Anfang der Folge als Beispiel:
- 1 / 1 = 1
- 2 / 1 = 2
- 3 / 2 = 1,5
- 5 / 3 = 1,6
- 8 / 5 = 1,6
- 13 / 8 = 1,625
- 21 / 13 = 1,615384615
Zwei Aspekte sind hier interessant: Erstens nähert sich der Quotient der Goldenen Zahl umso dichter, je weiter man in der Fibonacci-Folge fortschreitet. Zweitens Oszillieren die Werte um die Goldene Zahl. Das bedeutet sie liegen abwechselnd über und unter der Goldenen Zahl, immer aber wird der Abstand zur Goldenen Zahl geringer. Der Mathematiker sagt, die Werte konvergieren oszillierend zur Goldenen Zahl.
Hier ist der Zusammenhang mathematisch gut beschrieben: Bei Youtube diese Videonummer in die Suche eingeben: LDoKsw3SOdw
